Transformer:注意力机制(attention)和自注意力机制(self-attention)的学习总结_注意力机制和自注意力机制-CSDN博客
注意力机制的通俗理解
注意力机制其实是源自于人对于外部信息的处理能力。由于人每一时刻接受的信息都是无比的庞大且复杂,远远超过人脑的处理能力,因此人在处理信息的时候,会将注意力放在需要关注的信息上,对于其他无关的外部信息进行过滤,这种处理方式被称为注意力机制。
非自主提示和自主提示
针对于注意力机制的引起方式,可以分为两类,一种是非自主提示,另一种是自主提示。
其中非自主提示指的是由于物体本身的特征十分突出引起的注意力倾向
自主提示指的是经过先验知识的介入下,对具有先验权重的物体引起的注意力倾向。换句话说,可以理解为非自主提示源自于物体本身,而自主提示源自于一种主观倾向。举例说明如下:

当我们第一眼看到上图时,我们便会首先将注意力集中到兔子身上。这是因为,整张图中兔子的特征十分的突出,让人一眼就关注到兔子身上。这种引起注意力的方式便是非自主提示。
在看到兔子之后,我们便想兔子在干嘛,从而我们就会关注兔子的行为。此时兔子在吃草,这时我们便把注意力集中在兔子周边的草上。这种引起注意力机制的方式便是自主提示,其中"兔子在干嘛"则是我们主观意识。
注意力机制的进阶理解
另外,为加深理解,再引用一下动手学深度学习中的例子解释:
此时我们面前有五个物体,分别是报纸,论文,咖啡,笔记本和书。首先,我们会关注在咖啡身上,因为只有咖啡是红色,而其他物体是黑白。那么红色的咖啡由于其显眼的特征,就成了注意力机制的非自主提示。
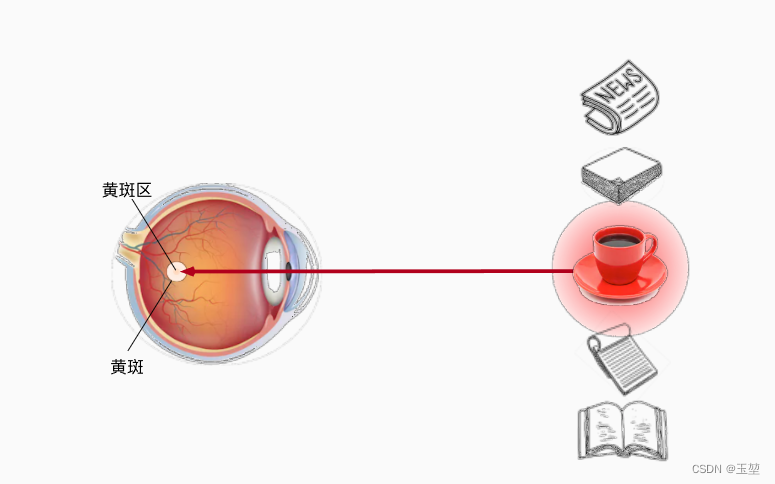
喝完咖啡后,十分精神,想看本书。此时,通过"想看书"这种意识,我们将注意力放到了书上。这种通过主观意识引起注意力的方式称为自主提示。
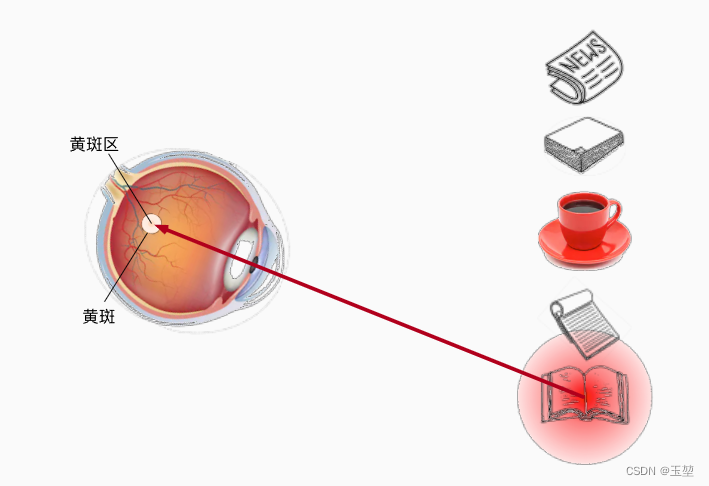
查询,键和值
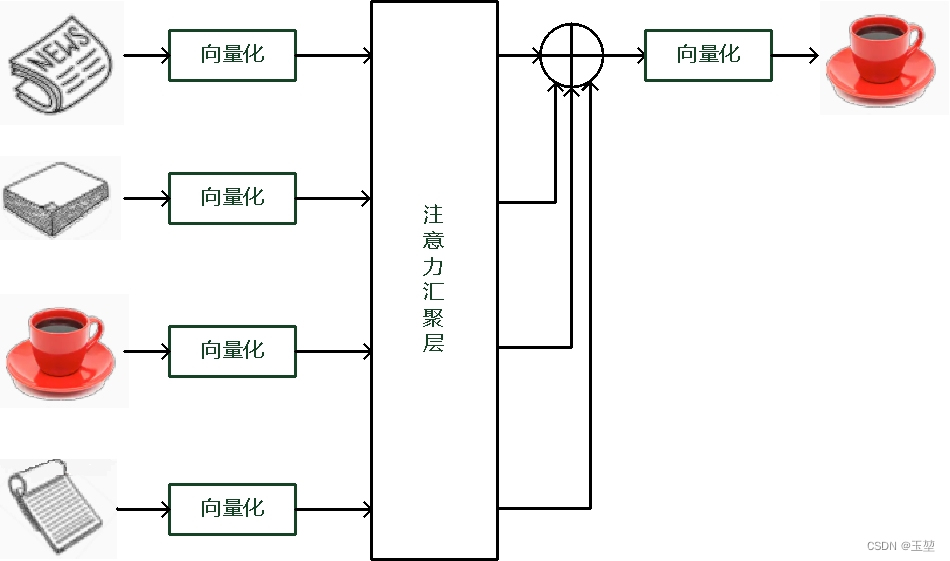
根据自主提示和非自主提示来设计注意力机制。首先考虑简单情况,即只考虑非自主提示的话,只需要对所有物体的特征信息(非自主提示)进行简单的全连接层,甚至是无参数的平均汇聚层或者最大汇聚层,就可以提取出需要感兴趣的物体。
下图是平均汇聚方法的示例图,最后结果是所有物体向量的平均加权和。(为什么平均加权最后还是能得出咖啡呢,因为咖啡本来的值就很大。可以这个么理解,数列[1,2,89,1],加权求和后对总体影响最大的还是89。)
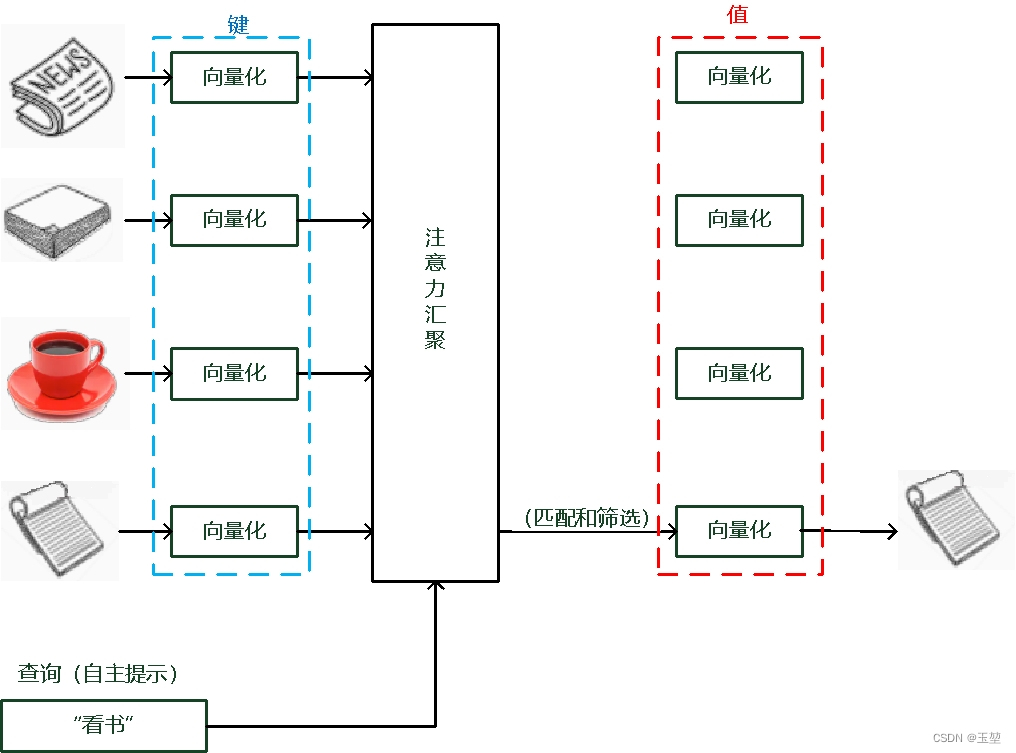
而如果考虑自主提示的话,我们就需要设计一种通过查询(Query),键(Key)和值(Value) 来实现注意力机制的方法。其中Query指的是自主提示,即主观意识的特征向量,Key指的是非自主提示,即物体的突出特征信息向量,Value则是代表物体本身的特征向量。
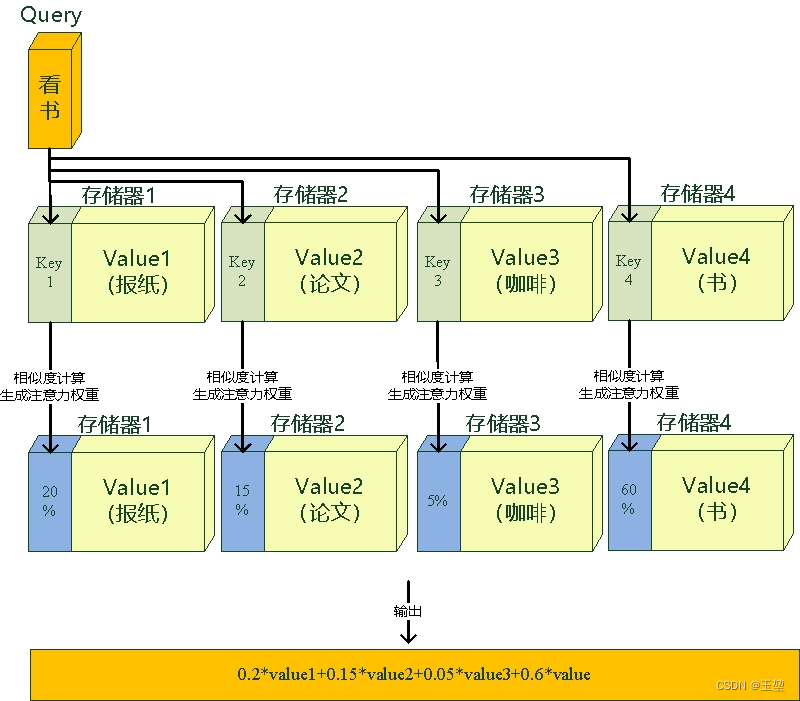
注意力机制是通过Query与Key的注意力汇聚(指的是对Query和Key的相关性进行建模,实现池化筛选或者分配权重),实现对Value的注意力权重分配,生成最终的输出结果。如下图所示:
另外,还有一种理解方式。我们可以将查询,键和值理解为一种软寻址(Soft Addressing)
Value可以看作存储器存储的内容,Key看作是存储器的地址。当Key==Query时,则取出Key地址对应存储器中的Value值,这被称为硬寻址。
而软寻址则是通过计算Key和Query的相似度来进行寻址,这种方法不只是获取一个Key地址中存储器的Value值,而是获取所有的存储器中的Value值的加权和 。至于每个Value的权重(重要程度),是通过Key和Query相似度计算得到的,最终的输出是所有Value值和其权重的加权和。如下图所示:
简单注意力机制的代码实现
训练一个神经网络来拟合一个函数。
数据集
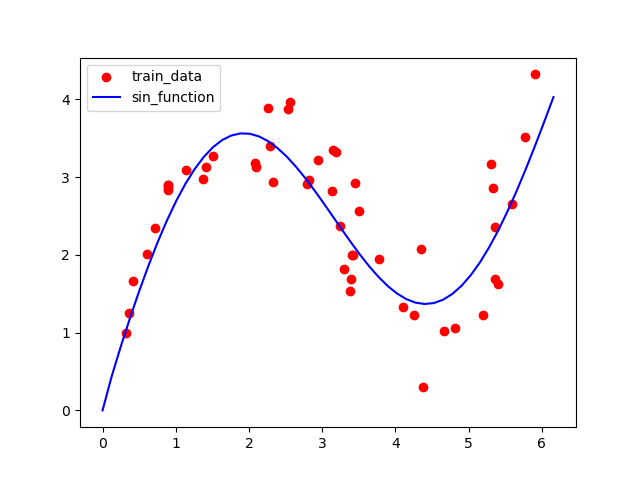
先通过python代码生成一组训练数据,生成方法如下公式:
y=sin(x)+x^{0.8}+ε
其中ε是自然噪声
import numpy as np
import matplotlib.pyplot as plt
def f(x):
"""
实现 y=sin(x)^2+x^0.8
:param x:训练数据x, 类型numpy(dim,)
:return: 训练标签y, 类型numpy(dim,)
"""
return np.sin(x) * 2 + x ** 0.8
if __name__ == '__main__':
# 生成训练数据和标签。
x_train = np.sort(np.random.rand(50)) * 6
y_train = f(x_train) + np.random.normal(0, 0.5, 50) # 这里加上了噪声ε
# 生成测试数据和真实标签。
x_test = np.arange(0, 6.28, 0.12566)
y_true = f(x_test)
# 绘制图像
plt.figure(1)
l1 = plt.scatter(x_train, y_train, color="r") # 红色曲线为训练数据
l2, = plt.plot(x_test, y_true, color="b") # 蓝色曲线为真实数据分布,即没有噪声项ε
plt.legend(handles=[l1, l2], labels=["train_data", "sin_function"], loc="best")
plt.savefig("data.png")
产生的效果如下图所示:
平均汇聚
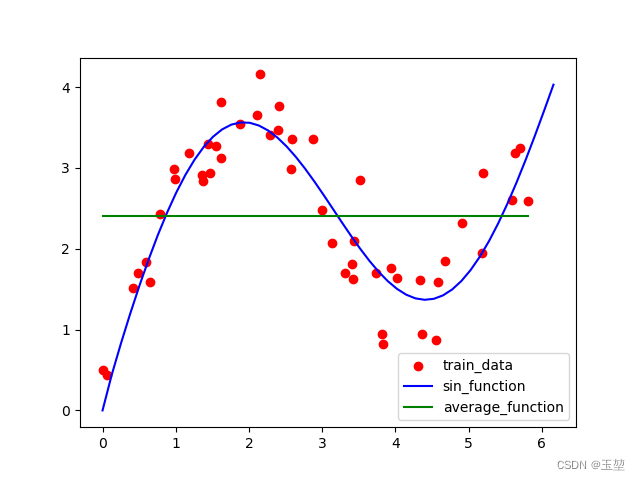
完全不考虑注意力机制的一种基底算法,简而言之就是对于任何一个点的预测,都采用求平均值的做法。
用到的公式为
f(x)=\frac{1}{n}\sum^{n}_{i=1}, i=1,2,3,...,50
当然结果也是很差的,算法就不详写了,下图绿色部分为预测出的曲线:
非参数的注意力汇聚(Nadaraya-Watson核回归)
求全局平均值确实是不合理的,但是会有一个思路,就是局部平均值会不会稍微合理点?
比如,我现在想要知道x=10处的值,那么我应该考虑的是x=10附近的值的样子,比如说我仅关注(5-15)之间的训练集的分布情况,除此以外就统统不考虑,这正是注意力的一种体现。
这里介绍一下之后算法的官方名字:非参数的注意力汇聚(Nadaraya-Watson核回归)。
推导的过程省略了,公式如下:
f(x)=\sum_{i=1}^{n}softmax(exp(\frac{1}{2}(x-x_i)^2))y_i
softmax激活函数可以将一系列的值转化成百分比概率,特性有以下两个:
-
值越大权重越大
-
一系列概率值相加和为1
先看一个demo代码理解一下算法的大致思想:
import numpy as np
def f(x):
# 这里拟合的函数是 2x + 1
return 2 * x + 1
def softmax(x):
# 即softmax激活函数
return np.exp(x) / np.sum(np.exp(x))
x_train = np.arange(1, 10, 2)
y_train = f(x_train)
print('看看数据集')
print(f'x: {x_train}')
print(f'y: {y_train}')
print('----------------------')
def attention_pool(query, key, value):
"""
非参数的注意力汇聚层的实现方法。
:param query:查询,即目前需要处理的参数
:param key:键
:param value:值
:return: 注意力汇聚的加权和,类型numpy(dim)。query中的元素,都是该元素通过该计算key的权重,和value的加权和。
"""
result = np.sum(np.dot(softmax(-(query - key) ** 2 / 2), value))
return result
def attention_value(query, key):
result = softmax(-(query - key) ** 2 / 2)
return result
print(f'注意力汇聚的结果:{attention_pool(6, x_train, y_train)}')
print(f'注意力权重(转化成百分比):{[str(round(i * 100, 2)) + "%" for i in attention_value(6, x_train)]}')
该代码输出如下:
看看数据集
x: [1 3 5 7 9]
y: [ 3 7 11 15 19]
----------------------
注意力汇聚的结果:12.999969831584712
注意力权重(转化成百分比):['0.0%', '0.9%', '49.1%', '49.1%', '0.9%']
代码不一一解析了,直观感受Nadaraya-Watson核回归的算法要义即是:关注临近值。
这里的key和value是我们预设的x,y,可以理解为这是真实世界的观测值。x的取值范围是[1 3 5 7 9]。那当我们给模型一个全新的值6时,首先交予attention机制算出注意力权重,即上述代码中的softmax(-(query - key) ** 2 / 2)这段。结果是['0.0%', '0.9%', '49.1%', '49.1%', '0.9%'],可以看出在最邻近6的值,5和7中,attention给了最多的权重。然后再将注意力机制的权重直接乘上真实样本y,即获取了x=6的时候y可能的值,算法结果是12.9。
import copy
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(233) # 固定随机种子使产生的数据一致
def f(x):
# 实现 y=sin(x)^2+x^0.8
return np.sin(x) * 2 + x ** 0.8
def softmax(x):
# 即softmax激活函数
return np.exp(x) / np.sum(np.exp(x))
def attention_pool(query, key, value):
"""
非参数的注意力汇聚层的实现方法。
:param query:查询,即目前需要处理的参数
:param key:键
:param value:值
:return: 注意力汇聚的加权和,类型numpy(dim)。query中的元素,都是该元素通过该计算key的权重,和value的加权和。
"""
for i in range(len(value)):
query[i] = np.sum(np.dot(softmax(-(query[i] - key) ** 2 / 2), value))
return query
def show_heapmap(query, key):
"""
计算注意力机制图。
:param query: 查询, 类型numpy(dim,)
:param key: 键, 类型numpy(dim,)
:return:注意力机制图,类型numpy(dim, dim)
"""
heapmap = []
for i in range(len(key)):
heapmap.append(softmax(-(query[i] - key) ** 2 / 2))
heapmap = np.array(heapmap)
return heapmap
def plot_figure():
# 一个绘画用的辅助函数
l1 = plt.scatter(x_train, y_train, color="r")
l2, = plt.plot(x_test, y_true, color="b")
l4, = plt.plot(x_train, sf_attention_function, color="black")
plt.legend(handles=[l1, l2, l4],
labels=["train_data", "sin_function", "average_function", "sf_attention_function"], loc="best")
plt.savefig("sf_average_function.png")
def plot_heap_map(heap_map):
# 画热力图的函数
plt.figure(2)
plt.imshow(heap_map)
plt.xlabel("x_train")
plt.ylabel("query_x")
plt.savefig("heapmap_no_param.png")
if __name__ == '__main__':
# 生成训练数据和标签。
sample_num = 50
x_train = np.sort(np.random.rand(sample_num)) * 6
y_train = f(x_train) + np.random.normal(0, 0.5, sample_num) # 这里加上了噪声ε
# 生成测试数据和真实标签。
x_test = np.arange(0, 6.28, 6.28/sample_num)
y_true = f(x_test)
query_x = copy.deepcopy(x_test)
sf_attention_function = attention_pool(query=query_x, key=x_train, value=y_train)
plot_figure() # 绘制图像
plot_heap_map(show_heapmap(query=x_test, key=x_train)) # 绘制query和key的交互热力图
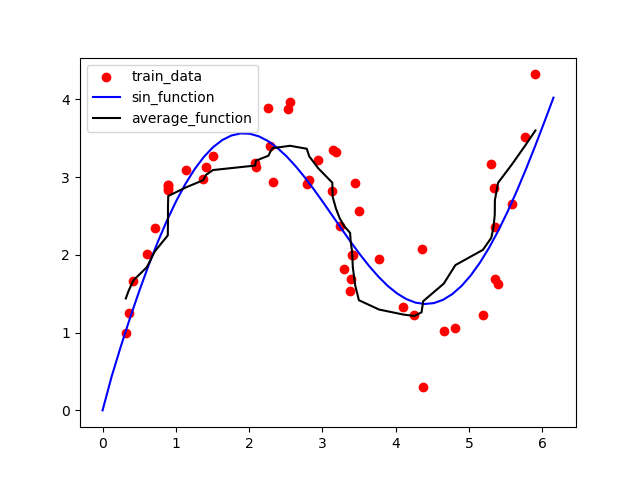
结果图如下:
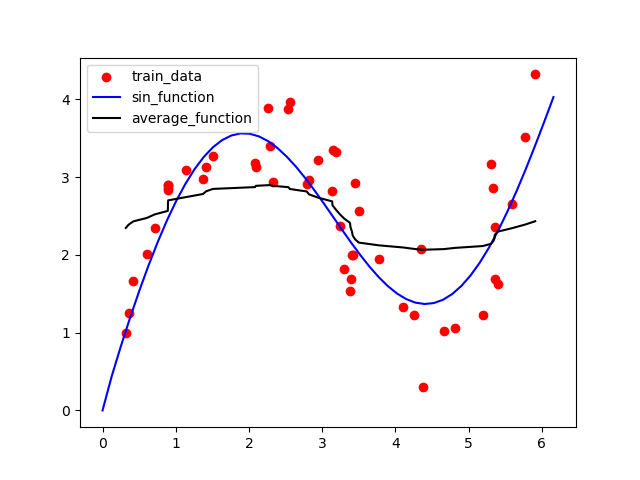
黑色的线是非参数注意力汇聚方法的结果,从上图可以看出其结果明显优于平局汇聚方法。
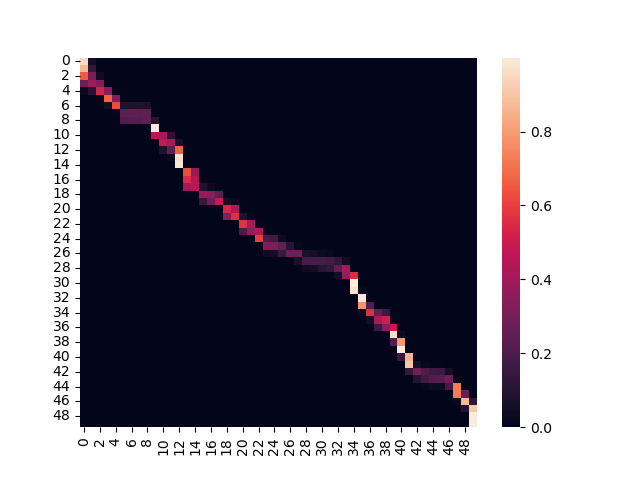
下图是注意力权重图。表示横轴Key和纵轴Query的权重关系,可以看出Query和Key值相似时,权重很大,其他情况权重很小。如下图所示:
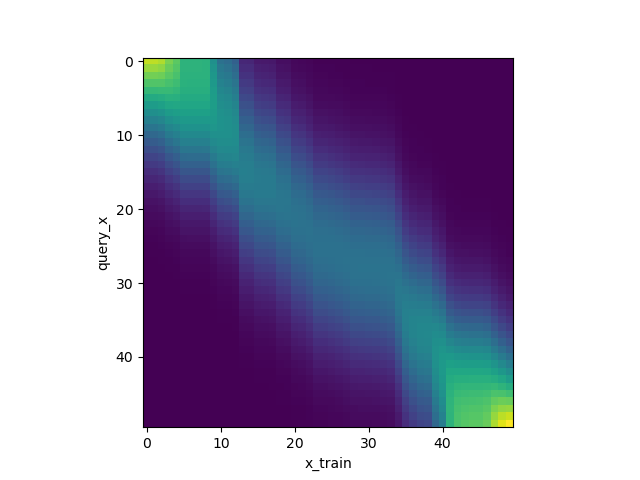
由于上述代码仅仅是个attention,并没有办法学习到全部的信息,如果要更优地拟合曲线,那就需要使用神经网络。
带参数的注意力汇聚(Nadaraya-Watson核回归)
我们也可以使用带参数的方法更好,更快的拟合目标函数。公式如下所示,其中ω是可学习的参数。
f(x)=\sum_{i=1}^{n}softmax(exp(\frac{1}{2}((x-x_i)ω)^2))y_i
模型的代码如下:
import os.path
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import seaborn as sns
np.random.seed(233) # 固定随机种子使产生的数据一致
class AttentionPoolWithParameter(nn.Module):
def __init__(self):
super(AttentionPoolWithParameter, self).__init__()
self.w = nn.Parameter(torch.rand((1,), requires_grad=True)) # 可学习的参数w。
self.attention_data = [] # 这是日后画图用的
def forward(self, q: "(1, 50)", k: "(1, 50)", v: "(1, 50)"):
"""
实现方法。
:param q: 查询, tensor(1,dim)
:param k: 键, tensor(1,dim)
:param v: 值, tensor(1,dim)
:return: 注意力权重和值的加权和, tensor(1,dim)
"""
# 通过复制将q的维度,扩展为(dim,dim),方便计算
q = q.repeat_interleave(k.shape[1]).reshape(-1, k.shape[1])
attention = torch.softmax(-((q - k) * self.w) ** 2 / 2, dim=1)
self.attention_data.append(attention.detach().numpy())
# torch.bmm是矩阵相乘.
return torch.bmm(attention.unsqueeze(0), v.unsqueeze(-1)).reshape(1, -1)
def f(x):
# y=sin(x)^2+x^0.8
return np.sin(x) * 2 + x ** 0.8
def softmax(x):
return np.exp(x) / np.sum(np.exp(x))
def show_heapmap(query, key):
"""
计算注意力机制图。
:param query: 查询, 类型numpy(dim,)
:param key: 键, 类型numpy(dim,)
:return:注意力机制图,类型numpy(dim, dim)
"""
heapmap = []
for i in range(len(key)):
heapmap.append(softmax(-(query[i] - key) ** 2 / 2))
heapmap = np.array(heapmap)
return heapmap
def plot_figure():
# 一个绘画用的辅助函数
l1 = plt.scatter(x_train, y_train, color="r")
l2 = plt.plot(x_test, y_true, color="b")
plt.legend(handles=[l1, l2, l5],
labels=["train_data", "sin_function", "sf_attention_function"], loc="best")
plt.savefig("attention_exp.png")
def plot_heap_map(heap_map):
# 画热力图的函数
plt.figure(2)
plt.imshow(heap_map)
plt.xlabel("x_train")
plt.ylabel("query_x")
plt.savefig("heapmap.png")
def plot_attention_heap_map(ats_list):
if not os.path.exists('data'):
os.mkdir('data')
index = 1
for i in ats_list:
fig = plt.figure()
hp = sns.heatmap(i)
plt.savefig(f"data/attention_heapmap_{index}.png")
index += 1
plt.close()
if __name__ == '__main__':
# 生成训练数据和标签。
sample_num = 50
x_train = np.sort(np.random.rand(sample_num)) * 6
y_train = f(x_train) + np.random.normal(0, 0.5, sample_num) # 这里加上了噪声ε
# 生成测试数据和真实标签。
x_test = np.arange(0, 6.28, 6.28 / sample_num)
y_true = f(x_test)
# 训练模型
net = AttentionPoolWithParameter()
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
loss_func = nn.MSELoss(reduction='none')
x_test_ts = torch.tensor(x_test.astype(np.float32)).reshape(1, -1)
y_true_ts = torch.tensor(y_true.astype(np.float32)).reshape(1, -1)
x_train_ts = torch.tensor(x_train.astype(np.float32)).reshape(1, -1)
y_train_ts = torch.tensor(y_train.astype(np.float32)).reshape(1, -1)
net.train()
for epoch in range(20):
optimizer.zero_grad()
y_pred = net(x_test_ts, x_train_ts, y_train_ts)
loss = loss_func(y_pred, y_true_ts)
loss.sum().backward()
optimizer.step()
print(f'epoch {epoch + 1}, loss {float(loss.sum()):.6f},parameter w:{net.w.data}')
net.eval()
with torch.no_grad():
y_pred = net(x_test_ts, x_train_ts, y_train_ts)
l5, = plt.plot(x_test.squeeze(), y_pred.squeeze(), color="pink")
plot_figure()
plot_attention_heap_map(net.attention_data)
heap_map = show_heapmap(x_test.squeeze(), y_pred.squeeze().numpy())
plot_heap_map(heap_map)
可以看到模型其实很简单,其实就是加了一个可变的参数ω,通过损失函数来直接控制权重,结果如下图,可以看到效果好得多。
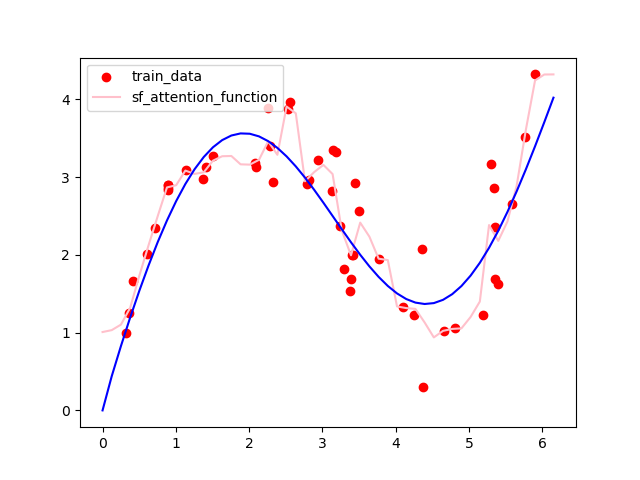
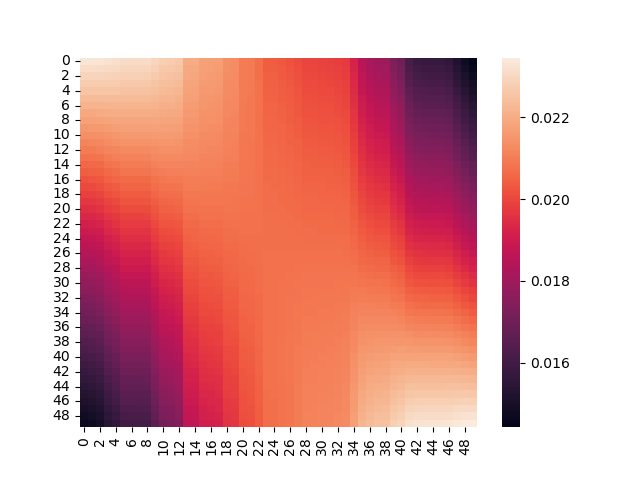
将attention的权重通过plt打印出来,可以发现一个明显的收缩趋势:
一开始是这样:
之后是这样:
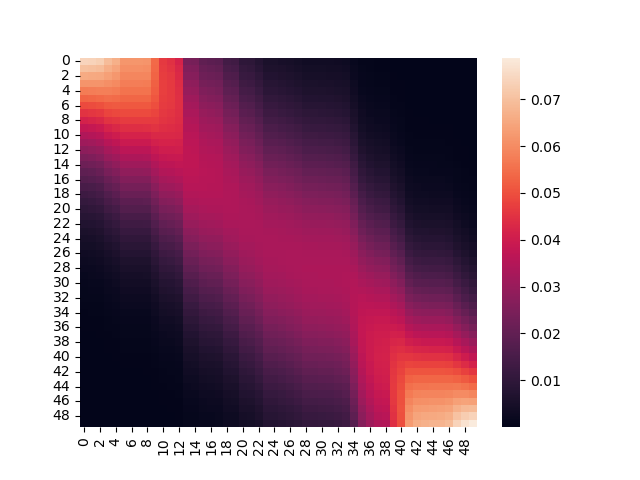
最后变成这样:
解释起来就是:最关心点周围一部分的值,并且将其作为预测的依据。将无参数的注意力汇聚代码中乘以一个系数,将系数设置为较大的值,也可以近似得到这样的效果,将上述非参数注意力汇聚的代码中的attention_pool函数进行如下改写:
def attention_pool(query, key, value):
for i in range(len(value)):
# query[i] = np.sum(np.dot(softmax(-(query[i] - key) ** 2 / 2), value)) 这是原本的公式
query[i] = np.sum(np.dot(softmax(-(query[i] - key) ** 2 * 5), value)) # 系数提高
return query
最终可以得到这样的结果:
可以看到效果媲美带参数的算法。
总结一下
经过上述几个例子。我们可以总结出一个通用的注意力机制公式:
f(x)=\sum_{i=1}^{n}a(query-key_i)values_i, i=1,2,3,4...n
其中的a(query, key_i)称为评分函数。用来对查询和键的关系进行数学建模,即实现查询和键的相关性计算,然后再经过softmax函数,即可得到查询和键的概率分布(即注意力权重)。最后,通过注意力权重和Value值进行加权,实现注意力分配或者结果筛选。
[文章导入自 http://qzq-go.notion.site/62cbee01c7aa4c4d90acb00010d2106a 访问原文获取高清图片]